Document ressource - Rugosité des surfaces usinées: Modélisation des défauts d'ordre 3

2. Généralités sur la rugosité des surfaces usinées

2.2. Modélisation des défauts d'ordre 3

Hypothèses de modélisation

Les défauts d'ordre 3 peuvent être modélisés par un raisonnement purement géométrique en assimilant ces défauts à la forme théorique de la surface effectivement engendrée par le déplacement du tranchant (arrêtes et faces de coupe) de l'outil dans l'espace de la pièce. Les hypothèses associées à cette modélisation sont :

La trajectoire de l'outil par rapport à la pièce est parfaite (celle programmée par l'opérateur).
La géométrie de la partie active de l'outil est conforme à celle définie par le fabriquant.

Dans le cas d'un chariotage (translation de l'outil parallèle à l'axe du cylindre usiné en tournage), la surface engendrée est un sillon hélicoïdal résultant de la forme du bec de l'outil et du mouvement hélicoïdal de l'outil par rapport à la pièce généré par la machine-outil.

Cas d'un angle de direction d'arrête secondaire κ' important

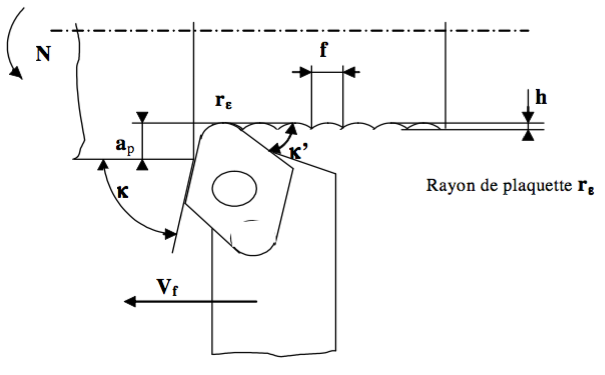
Interaction cercle / cercle

Fig 2.2.1. Calcul de la rugosité théorique à partir d'une Interaction cercle/cercle

Dans le cas de la figure 2.2.1, nous nous plaçons dans un plan orthogonal à la vitesse de coupe Vc, la forme du sillon est définie par l'interaction du rayon de bec Rε de l'outil avec la trace laissée par celui-ci au tour précédent. L'outil se déplaçant de la valeur de l'avance f lors d'un tour de la pièce.

La connaissance de f et Rε permet de calculer la profondeur h des sillons.

Ainsi, pour un profil en arcs de cercle obtenu avec un outil à bec rond de rayon Rε et possédant un angle de direction de l’arête secondaire κ’ suffisant, la profondeur h est donnée par la relation :

\( h=R \epsilon-R \epsilon \sqrt{1- ( \frac{f}{2R \epsilon} )^2} \simeq \frac{f^2}{8R \epsilon}~si~f \ll R \epsilon \)

La valeur de h est un ordre de grandeur de la rugosité totale "théorique" Rtth.

Ainsi, d'après cette modélisation, ces sillons ont un profil d'autant plus profond que le rayon du bec de l'outil est plus faible. Par ailleurs, ils sont d'autant plus larges que l'avance par tour est grande.

Cas d'un angle de direction d'arrête secondaire κ' faible

dfc

Fig 2.2.3. Calcul de la rugosité théorique à partir d'une Interaction cercle/plan

Dans le cas de la Figure 2.2.3, la géométrie du sillon ne provient plus d'une interaction entre surfaces usinées par le rayon de bec mais plutôt par le rayon de bec et l'arrête secondaire. Dans ce cas, la rugosité théorique s'écrit :

\( h=R \epsilon(1-cos( \kappa'))+fcos( \kappa')sin( \kappa')-fsin^2( \kappa') \sqrt{\frac{2R\epsilon }{fsin(\kappa')}-1} \)