Document ressource - Usure des outils de coupe

Définition

L'étude d'un plan complet consiste à étudier toutes les combinaisons possibles des facteurs pris en considération dans l'expérience. Pour k facteurs à n niveaux, le plan complet comporte donc n^k essais. 

Pour illustrer l'étude des plans complets nous allons prendre comme exemple l'influence des conditions cinématiques de l'usinage (V_c et f) sur la durée d'outil T avec seulement 2 niveaux par facteur. Le plan complet comporte donc 4 essais (fig.9).

La réponse, caractéristique de la durée d'outil, diminue de 1 quand l'avance passe du niveau 1 au niveau 2 ; elle diminue de 1,5 quand la vitesse passe du niveau 1 au niveau 2. 

L'effet global de l'avance est de -1 et celui de la vitesse est -1,5.

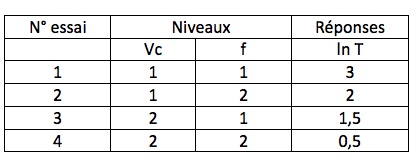
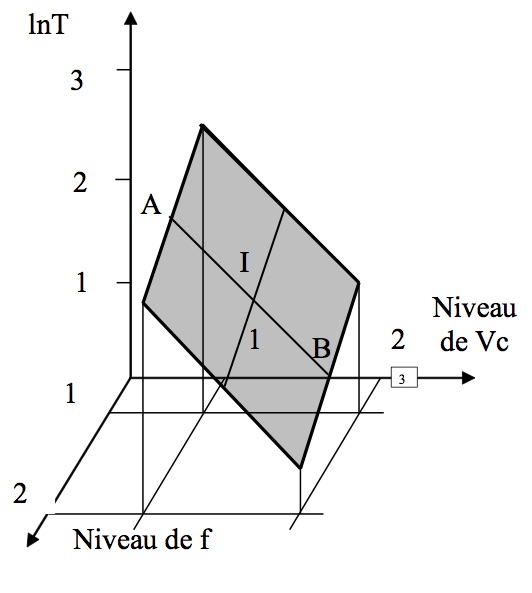
Fig.9

Calcul des effets moyens

Les effets moyens sont calculés par rapport à la moyenne générale des essais qui correspond au point central du domaine de validité des facteurs (point I sur Fig. 10)

L'effet moyen de l'avance au niveau 2 est obtenu par :

Ef2 = moyenne des réponses pour f au niveau 2 – moyenne générale ;

de même :

Ef1      = moyenne des réponses pour f  au niveau 1 – moyenne générale ;

EVc2    = moyenne des réponses pour Vc au niveau 2 – moyenne générale ;

EVc1    = moyenne des réponses pour Vc au niveau 1 – moyenne générale.

Exemple précédent : 

Moyenne = 1/4 * (3+2+1,5+0,5) = 1,75

EVc1 = 1/2 * (3+2)-1,75 = 0,75

EVc2 = 1/2 * (1,5+0,5)-1,75 = -0,75

Ef1 = 1/2 * (3+1,5)-1,75 = 0,5

Ef2 = 1/2 * (2+0,5)-1,75 = -0,5

Ef1 = -Ef2 et EVc1 = -EVc2. Il y a donc une seule valeur indépendante soit un seul degré de liberté par facteur.

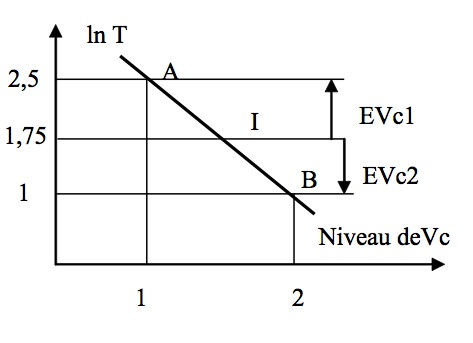
Fig.10

Calcul de la durée d'outil théorique

Connaissant les effets moyens des facteurs Vc et f, il est alors facile de calculer la durée d'outil théorique, c'est-à-dire la durée que l'on devrait mesurer si celle-ci ne dépendait que des effets moyens des facteurs pris en compte.

Exemple : essai n°2 (Vc au niveau 1 et f au niveau 2)

Durée théorique = moyenne générale + EVc1 + Ef2 =1,75 + 0,75 – 0,5 = 2

Dans cet exemple simple, la durée théorique est identique à la durée mesurée car nous avions choisi volontairement des valeurs de durées mesurées telles que les points soient situés sur le plan T(Vc,f), (fig.10).

En réalité, compte tenu de la précision du modèle de la loi d’usure et des dispersions liées aux résultats des essais d'usure, il existe des écarts entre les valeurs mesurées et théoriques.

Graphe des effets moyens

Le graphe des effets moyens est une représentation graphique des résultats du plan d'expériences (fig.11). Le sens de variation indique si les facteurs agissent de façon positive ou négative sur la réponse (ln(T)), la pente permet d'identifier rapidement le facteur le plus influent.

Dans notre exemple, les 2 facteurs (Vc et f) ont des effets défavorables sur la durée de vie de l'outil et le facteur Vc est le plus influent.

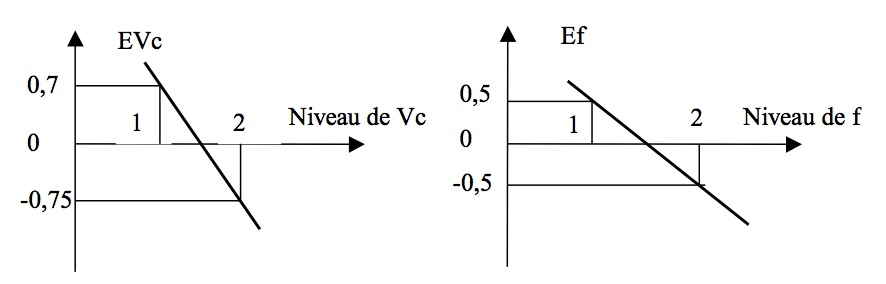
Fig.11 Graphe des effets moyens 

Notion d'interaction.

Les interactions sont les phénomènes les plus difficiles à interpréter. La figure 12 illustre cette notion.

Le cas (a) correspond à l'exemple précédent, il n'y a pas d'interaction car l'effet sur la durée d'outil est de –1.5 lorsque le facteur Vc passe du niveau 1 au niveau 2, et ceci indépendamment du niveau du facteur f.

Le cas (b) montre un phénomène d'interaction, il y a une distorsion de la surface de réponse d'autant plus grande que l'interaction est importante.

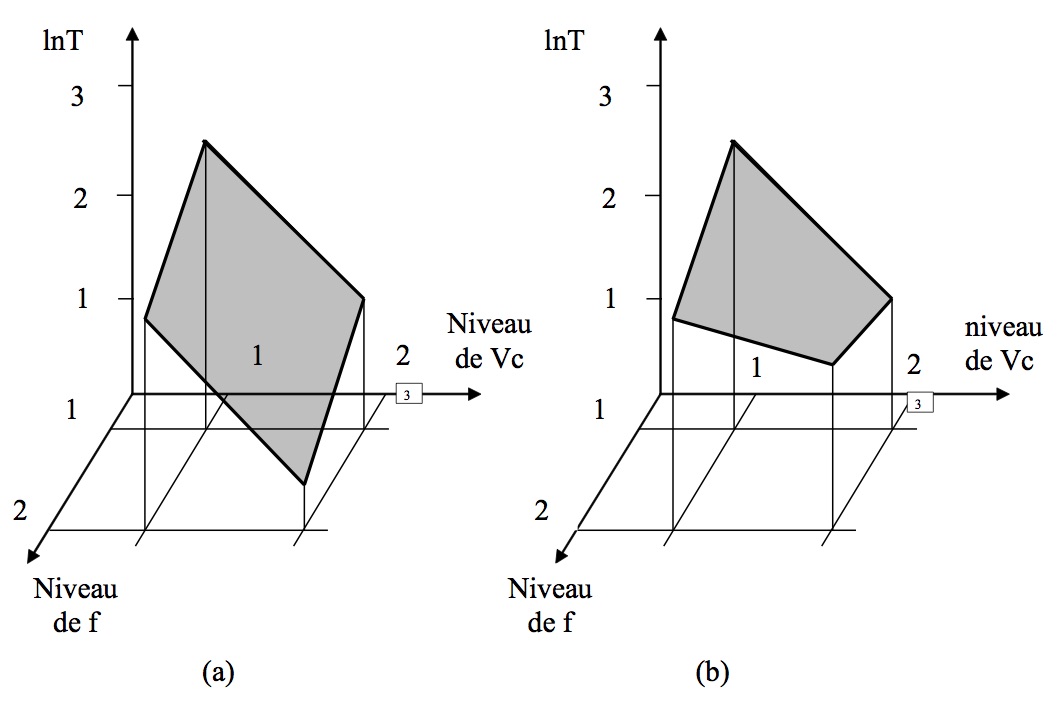
Fig.12 Notion d'interaction

Plan d'expérience fractionnaires. 

Dans les plans factoriels chaque nœud du maillage donne lieu à un essai, le nombre d'essais peut très vite devenir incompatible avec les contraintes industrielles.

La méthode des plans d'expériences fractionnaires permet de réduire de façon significative le nombre d'essais ; le principe consiste à n'étudier que certains points du maillage.

Ces plans doivent vérifier deux conditions : 

•   Première condition :

Ils doivent être orthogonaux pour calculer les effets d'un facteur indépendamment des autres facteurs. Il y a orthogonalité si à chaque niveau d'un facteur, tous les niveaux des autres facteurs sont associés le même nombre de fois dans le plan d'expériences.

Exemple : table de TAGUCHI L₉(3³), 9 essais, 3 facteurs (Vc, f, a_p) avec 3 niveaux (1, 2, 3).

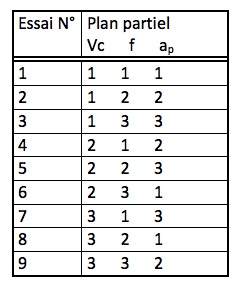
Tab.2

Essais 1, 2, 3 : Lorsque Vc est au niveau 1, f est une fois aux niveaux 1, 2 et 3 et de même pour le facteur a.

Essais 2, 5, 8 : Lorsque f est au niveau 2, Vc est une fois aux niveaux 1, 2, 3 et de même pour le facteur a.

Etc……

• Deuxième condition :

Condition sur le nombre de degrés de liberté. C'est le nombre de valeurs qu'il est nécessaire de calculer pour connaître l'ensemble des coefficients du modèle ; il est donc nécessaire de faire autant d'essais qu'il y a de degrés de liberté dans le modèle.

Exemple précédent :

•  soit le modèle T = Moyenne générale + EVc + Ef + Ea_p ,
•  avec 3 niveaux pour chaque facteur.

Pour déterminer les effets moyens du facteur Vc pour les trois niveaux, il suffit de calculer les effets moyens pour 2 niveaux car :

EVc1 + EVc2 + EVc3 = 0

Il y a donc 2 degrés de liberté pour EVc, de même pour Ef et Ea_p. 

Le nombre total de degrés de liberté de ce modèle est donc de 1+2+2+2 = 7.

Détermination de la loi d'usure des outils de coupe.

La loi d'usure des outils de coupe définit la variation du temps effectif de coupe T(min) en fonction des facteurs principaux de l'usinage : la vitesse de coupe Vc (m/min), l'avance par tour f (mm/tr) et la pénétration a_p (mm). Pour les valeurs usuelles de ces trois facteurs, la loi d'usure est généralement représentée par le modèle suivant:

\( T = K a_p^l f^m V_c^n \)

où K est un coefficient fonction du couple outil-pièce et du critère d'usure adopté, les exposants l, m, n dépendent essentiellement du matériau outil.

Par le changement de variables : A = ln(a_p), F = ln(f),  V = ln(Vc), on obtient le modèle linéaire suivant :

\( ln(T) = ln(K)+l A + mF + n V \)

D'autre part, si dans le modèle :

ln(T) = moyenne générale +EA+EF+EV

les effets moyens EA, EF et EV varient linéairement respectivement en fonction des facteurs A, F et V, on peut écrire :

EF = a2 F + b2

EV = a3 V + b3

En comparant les deux modèles de la loi d'usure, il vient :

ln(K ) = Moy + b1 + b2 + b3

l = a1

m = a2

n = a3

Le calcul des effets moyens EA, EF et EV des 3 facteurs A, F et V permet donc de déterminer aisément les valeurs des coefficients du modèle de la loi d'usure des outils de coupe.