Imprimer tout le livreImprimer tout le livre

Document ressource - Usure des outils de coupe

Site: Plateforme pédagogique Moodle
Cours: GM-3-S2-EC-PROFA : Procédés de fabrication et mise en forme pour la conception
Livre: Document ressource - Usure des outils de coupe
Imprimé par: Visiteur anonyme
Date: dimanche 22 décembre 2024, 17:18

Description

Document ressource sur l'usure des outils de coupe.

Les objectifs du TP associé sont:

  • observation d’un phénomène d’usure d’un outil de coupe, et sa prise en compte dans la mise en place d’une production.
  • observation de l'évolution de l'usure des outils à plaquette carbure et 
  • détermination des coefficients du modèle de la loi d'usure à partir d'un plan d'expériences.


Table des matières

1. Généralités sur l'usure des outils de coupe

 

1.1. Evolution de l'usure des outils de coupe

L'usure de l'outil se manifeste essentiellement sous deux aspects (Fig.1) :

  • L'usure "en cratère" sur la face de coupe de l'outil, par frottement du copeau. Au cours de l'usure, la profondeur "KT" et la position du cratère évoluent et influent, en particulier, sur le rayon d'enroulement du copeau ; le flanc arrière du cratère pouvant jouer le rôle d'un brise-copeau naturel.
  • L'usure frontale sur les faces en dépouille, par frottement sur la pièce. Elle se manifeste par l'apparition d'une bande brillante et striée, parallèle à l'arête. Dans la zone B, la largeur "VB" de cette bande évolue (dans le temps) parallèlement à la profondeur "KT" du cratère jusqu'à la destruction de la pointe par la conjonction de ces deux effets.

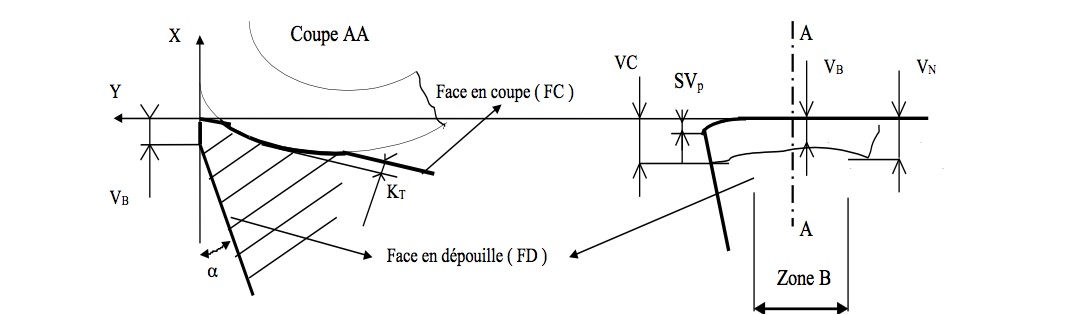
Fig.1: Définition des principaux paramètres caractéristiques de l'usure (Suivant Normes NF et I.S.O).

Fig.1: Définition des principaux paramètres caractéristiques de l'usure (Suivant Normes NF et I.S.O).

A noter toutefois :

  • l'accroissement de la largeur de la bande d'usure à ses extrémités, due à l'usinage des zones superficielles de la pièce, qui donne lieu à des phénomènes particuliers ;
  • dans des conditions de coupe sévères, l'apparition d'une déformation plastique de la pointe de l'outil caractérisée par son affaissement "SVP" ;
  • dans le cas de chocs répétés ou de variations périodiques des efforts (coupe discontinue, vibrations) la possibilité d'un effritement de l'arête de coupe.

Les mesures de l’usure frontale "VB" en fonction du temps de coupe (Fig.2) permettent en général de suivre l'évolution de l'usure. Cette évolution n'est pas rigoureusement continue et des irrégularités peuvent apparaître autour de la courbe traduisant la tendance moyenne.

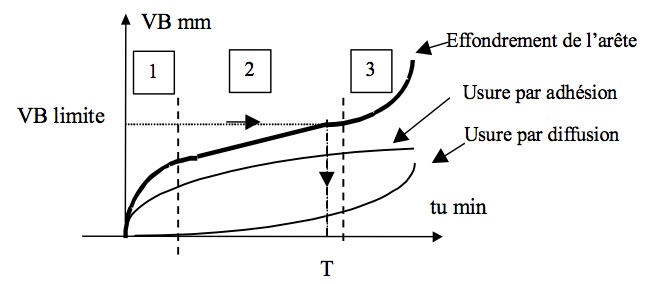
Fig.2 : Évolution de l’usure frontale

Fig.2 : Évolution de l’usure frontale


Dans le cas des outils carbures, on explique l’évolution de cette usure par la superposition de deux types principaux d’usure :

  • l’usure par adhésion favorisée par les pressions locales et les températures importantes.
  • l’usure par diffusion, transfert de certains constituants de l’outil dans le copeau, favorisée par les fortes températures à l’interface outil/copeau.

On observe 3 zones :

Zone 1 : période d’adaptation du tranchant au régime de coupe.

Zone 2 : Stabilisation du gradient d’usure, évolution sensiblement linéaire en fonction du temps.

Zone 3 : croissance rapide de l’usure qui précède l’effondrement de l’arête ; dans cette zone les risques de rupture d’outil sont importants.


1.2. Critères d'usure

Les critères usuellement utilisés pour les outils en carbure et, notamment, ceux recommandés par la norme NF E 66 505, sont basés sur l'évolution de l'usure frontale ou de la cratérisation. Du point de vue pratique, l'usure frontale est la plus importante à considérer, puisqu'elle détermine l'état de surface de la pièce usinée et la précision dimensionnelle.

De plus, l'expérience montre que l'évolution de l'usure des outils à plaquette carbure dite "à jeter", qui permettent de vitesses de coupe élevées, peut être définie de façon satisfaisante par la seule mesure de l'usure frontale, dans une large plage des paramètres de coupe. Toutefois, pour des valeurs élevées des paramètres de coupe provoquant une forte élévation de la température à l'interface outil-copeau, l'accélération de l'usure par diffusion devient très sensible, et favorise une évolution rapide de la cratérisation.

Le critère principal défini pour les outils carbure et céramique est le suivant :

  • largeur de la bande d'usure frontale VB = 0,3 mm si elle est uniforme dans la zone B ;
  • sinon, largeur maximale de cette bande VB = 0,6 mm.

Ces valeurs limites de VB correspondent sensiblement à celles relevées à la frontière des zones 2 et 3 de la figure 2, on minimise ainsi le risque de rupture accidentelle de l’outil pendant la production.


1.3. Loi d'usure des outils de coupe

Définition

La loi d'usure définit la variation de la durée effective de coupe T des outils en fonction des conditions géométriques et cinématiques de l'usinage. La durée effective de coupe T est définie comme étant le temps d'usinage qui conduit à l'usure limite définie par le critère d'usure précédent.

De nombreux modèles mathématiques ont été proposés pour représenter la loi d'usure des outils de coupe, parmi lesquels le modèle de TAYLOR généralisé :

\( T=K.a_p^l . f^m . V_c^m \)

Pour une géométrie de copeau donnée (f = cste et a = cste) ; il vient :

\( T=C.V_c^n \)

Ce modèle reflète correctement la moyenne des résultats expérimentaux dans la plage des paramètres de coupe couramment utilisés, mais peut s'écarter rapidement de la réalité en dehors du domaine usuel (Fig.3).

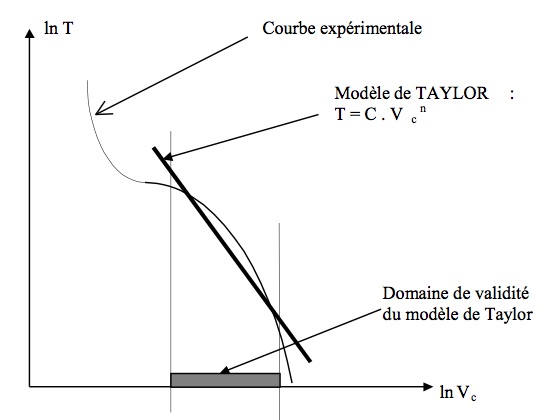
Fig.3 : Loi d'usure.

Fig.3 : Loi d'usure.


Détermination de la loi d'usure

La détermination des coefficients du modèle de la loi d'usure se fait à partir d'essais à paramètres de coupe constants. Chaque courbe d'usure frontale en fonction du temps de coupe permet de définir un point figuratif de la loi d'usure. Pour déterminer l'influence des trois conditions de coupe (pénétration, avance, vitesse de coupe) il est nécessaire d'effectuer un nombre minimal d'essais.

Nous utiliserons un plan d'expériences fractionnaire comportant 9 essais qui permet de tester 3 valeurs des 3 conditions de coupe dans le cas où il n'y a pas d'interaction entre elles. La réalisation complète de ces essais ne peut se faire dans le cadre d'un TP de courte durée ; aussi, un seul essai sera effectué. La détermination de la loi d'usure se fera à l'aide du résultat de cet essai et des résultats obtenus antérieurement.



2. Choix des conditions d'usinage - optimisation

 L'usinage par enlèvement de copeaux représente aujourd'hui, en France, 5% du PIB, sous réserve d'une bonne organisation et d'un environnement efficace, une machine-outil produit pendant 70 à 80% de son temps. L'un des enjeux actuels est d'optimiser ce temps pour améliorer la productibilité, le choix rationnel des conditions de coupe concourt largement à cet objectif.

Les principaux critères d’optimisation sont :

  1. Coût global de fabrication minimal
  2. Production horaire maximale
  3. Durée effective de coupe de l’outil imposée

2.1. Coût de fabrication minimal

La vitesse de coupe économique Véc est celle qui conduit au coût global par pièce usinée minimal. Ce coût se décompose de la façon suivante :


  • Coûts annexes par pièce Ca, indépendants des conditions de coupe. Ce sont essentiellement les frais résultant des opérations annexes effectuées avant ou après l'usinage de chaque pièce (montage, démontage, réglages, contrôle,…), et qui sont indépendants des conditions de coupes adoptées. Pour un travail déterminé, ces dépenses par pièce sont constantes, et fonction du coût horaire (ou "minute") du poste de travail.
  • Coûts d'usinage par pièce Cu : \( C_u = p_u . t_u \), avec pu le coût machine par minute et tu le temps d’usinage. Le coût minute du poste comprend :
    • les coûts de main-d'œuvre d'usinage (personnel conduisant la machine) ;
    • l’amortissement de la machine (ventilation des frais d'achat et installation par heure d'utilisation, déterminée a priori d'après la durée de vie probable de la machine) ;
    • les frais de maintenance, et divers.
  • Coût d'outillage Co (quote-part nécessaire pour l'usinage d'une pièce) : \( C_o = \frac{p_o}{T/t_u} \), avec po le prix de revient d’une arête de coupe (€) et T la durée de vie de l’outil (min). Le prix de revient d’une arête de coupe comprend :
    • les frais d'achat des outils, l'amortissement des porte-outils ;
    • les frais d'affûtage, l'amortissement du matériel d’affûtage ;
    • les frais de réglage.

Le rapport (T/tu) représente le nombre de pièces usinées par une arête.

  • Coût du changement d'arête Cc : \( C_c = t_c . \frac{p_u}{T/t_u} \). Il dépend du temps de changement d’arête tc et du coût minute du poste de travail.

Soit globalement

\( C_g = C_a + C_u + C_o + C_c = C_a + p_u . ( t_u + t_u \frac{t_c + Z}{T}) \)

avec Z = po/pu, qui caractérise l'importance relative des coûts d'outillage et d'usinage, laquelle dépend des conditions particulières de chaque poste de travail.

Le temps d'usinage d'une pièce tu et la durée effective de coupe T de l'outil sont liés aux conditions de coupe par les relations :

\( t_u = \frac{L}{N.f} \)

où \( N = \frac{1000 V_c}{\pi D} \).

Le modèle de Taylor généralisé donne:

\( T = K . a_p^1 . f^m . V_c^n \)

d'où

\( C_g = C_a + \frac{p_u L x D}{1000 f V_c} (1+(t_c+Z)/C_V V_C^n) \)

avec \( C_v = K a_p^1 f^m \).

Pour une profondeur de passe donnée (ap = ap1), l'évolution du coût global de fabrication en fonction de l'avance et de la vitesse de coupe est représentée graphiquement par une surface en forme de gouttière dont le fond est continuellement décroissant quand l'avance croît : le minimum du coût est alors obtenu pour la valeur maximale possible de l'avance (Fig.4).

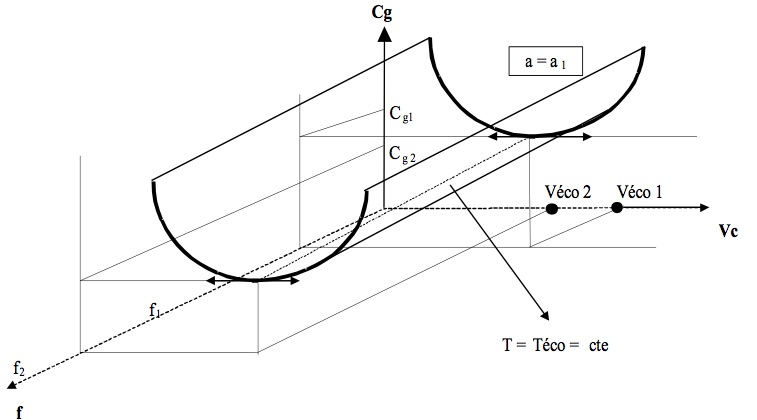
Fig.4: Coût global en fonction de la vitesse de coupe et de l’avance

Fig.4: Coût global en fonction de la vitesse de coupe et de l’avance

Pour une avance donnée ( f = f1), les évolutions du coût global et des différents coûts partiels sont indiqués sur la Fig.5.

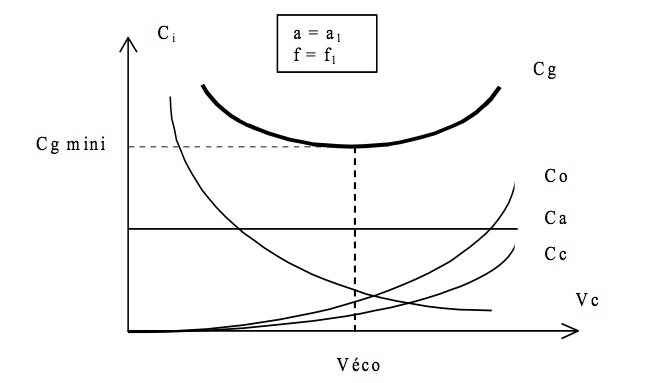
Fig.5 : Coûts en fonction de la vitesse de coupe

Fig.5 : Coûts en fonction de la vitesse de coupe

Le coût global par pièce est minimal pour la valeur de la vitesse de coupe Vec dite "économique", solution de l'équation différentielle :

\( \frac{\partial C_g}{\partial V_c} = 0 \) pour ap=ap1 et f=f1, soit 

\( V_{ec} = \left \lbrack \frac{(-n-1). (t_c+p_o/p_u)}{C_v} \right \rbrack ^{1/n} \)

avec \( C_v = K a_{p1}^l f_1^m \).

La durée effective de coupe de l'outil correspondante, dite "économique" est :

\( T_{ec} = (-n-1) . (p_o/p_u + t_c) \)

La valeur de la durée de coupe économique Tec est indépendante de la constante Cv, elle n'est donc pas fonction du matériau usiné, ni de la géométrie du copeau.

Par contre, Tec dépend de l'exposant n, c'est-à-dire du matériau outil (fig. 6). Les valeurs de Tec pour chaque matériau outil sont en moyenne :

  • Acier rapide : Tec ∈ [40 ; 120]min
  • Carbure : Tec ∈ [15 ; 40]min
  • Céramique : Tec ∈ [5 ; 15]min

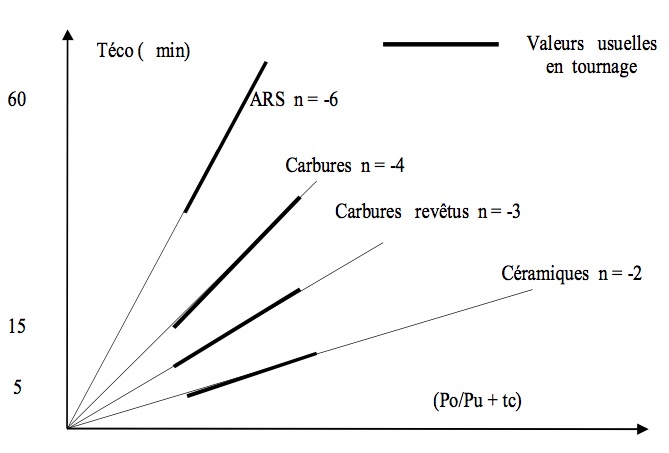
Fig.6: Tec = f (po/pu + tc)

Fig.6 : \( T_{ec} = f(\frac{p_o}{p_u} + t_c) \)

Ainsi, les valeurs des vitesses de coupe indiquées dans les tableaux des données correspondent généralement à une durée effective de coupe voisine de l'optimum économique. La détermination des vitesses de coupe pour une durée effective de coupe différente se fait facilement à partir du modèle de Taylor.








2.2. Production maximale

Le volume horaire de production Q varie de façon inverse au temps d'usinage, il augmente donc lorsque la vitesse de coupe augmente. Néanmoins, si l'on augmente très fortement cette vitesse, l'usure de l'outil devenant très rapide, il sera alors nécessaire d'interrompre fréquemment l'usinage pour le remplacement de l'arête, et le gain de temps-copeaux sera alors neutralisé par la perte de temps pour ce remplacement. La surface Q = f(Vc, f) représentée sur la Fig.7 montre que la valeur maximale du volume horaire croit lorsque l’avance augmente.

Le volume horaire maximal est alors obtenu pour la valeur maximale possible de l'avance.

Pour une avance donnée le volume horaire est maximal pour la vitesse de coupe Vq. Le choix de cette vitesse de coupe, dans une fabrication en série, conduit à la plus grande production, mais pour un coût de fabrication plus élevé que celui donné par la vitesse économique.

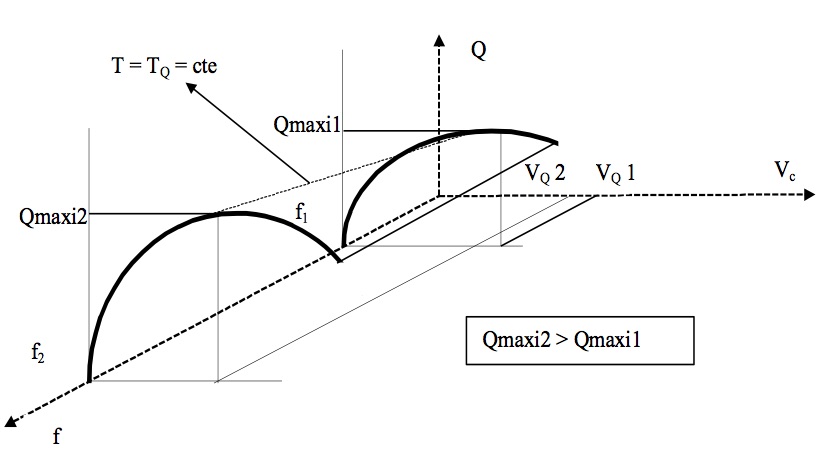
Fig.7.Volume de production horaire en fonction de la vitesse de coupe.

Fig.7.Volume de production horaire en fonction de la vitesse de coupe.


Vitesse et durée effectives de coupe de production maximale

Le temps total d'usinage d'une pièce est donné par :

\( TU = t_u + t_c \frac{t_u}{T} + t_a \) (en minutes)

avec 

  • tu : temps d'usinage (temps copeaux)
  • \( t_c\frac{t_u}{T} \) : temps de changement d'arête rapporté à une pièce
  • ta : temps annexe par pièce (montage, démontage,...)

Le volume horaire de production exprimé en nombre de pièces par heure est alors donné par :

Q = 60 / TU (pièces par heure)

Le volume horaire Q sera maximal pour la valeur Vq de la vitesse de coupe solution de l'équation différentielle :

\( \frac{\partial Q}{\partial V_c} = 0 \) pour ap = ap1 et f=f1

soit  

\( V_q = \left \lbrack \frac{C_v}{(-n-1)t_c}\right \rbrack ^{-1/n} \)

avec \( C_v = K a_{p1}^lf_1^m \)

La durée effective de coupe correspondante est :

\( T_q = (-n-1)t_c \)

Comme pour la valeur de la durée économique Tec, la valeur de durée de production maximale Tq est indépendante de la constante Cv ; elle n'est donc pas, en première approximation, fonction du matériau usiné, ni de la géométrie du copeau.

Par contre, Tq dépend de l'exposant n du modèle de Taylor c'est-à-dire du matériau outil. Elle dépend aussi du temps de changement d'arête tc.

2.3. Durée effective de coupe imposée

Dans les usinages en grande série, on impose souvent une durée d'outil correspondant à une séance de travail ; les outils en service étant systématiquement échangés contre des outils neufs en fin de série. Ou encore, une durée d'outil déterminée par l'importance de la série de pièces à usiner, l'outil étant alors systématiquement échangé à la fin de chaque série.

En travaillant ainsi à "durée imposée", on abandonne volontairement le régime économique ou le régime de production maximale ; on consent ainsi à une majoration du coût de l'usinage et à une perte de production pour bénéficier en contrepartie, de facilités de distribution, de montage et d'entretien de l'outillage. Il est bon, toutefois, de s'assurer que cette contrepartie est globalement suffisante pour justifier la perte ainsi consentie au niveau du coût d'usinage.


3. Plan d'expérience pour l'étude de l'usure des outils de coupe

La méthode des plans d'expériences n'est pas une technique nouvelle, mais il a fallu attendre les travaux du Docteur TAGUCHI au Japon pour qu'elle soit plus largement utilisée. Cette méthode permet une diminution souvent importante du nombre d'essais par rapport aux techniques traditionnelles de tâtonnements successifs.

Supposons que l'on désire étudier l'influence des conditions cinématiques de l'usinage sur la durée de vie T des outils de coupe. Chacun des facteurs (vitesse de coupe Vc et avance f) peut prendre plusieurs valeurs comprises entre un mini et un maxi.

La démarche traditionnelle, définie par les normes ISO, consiste à étudier séparément les deux facteurs Vc et f. On fixe f à un niveau moyen et on détermine la valeur de la durée de vie de l'outil lorsque Vc varie de sa valeur mini à sa valeur maxi à l'aide de 5 expériences par exemple. On procède de même pour étudier l'influence de l'autre facteur f.

Ces essais permettent de savoir comment agit Vc quand f est au niveau moyen, mais ne permettent pas de connaître son action quand f est au niveau mini ou maxi.

Pour ce faire, il est nécessaire de réaliser un maillage du domaine de validité des deux facteurs Vc et f et d'exécuter un essai à chacun des nœuds du maillage (fig.9) ; il faut alors réaliser 25 expériences pour connaître la loi T(Vc, f).

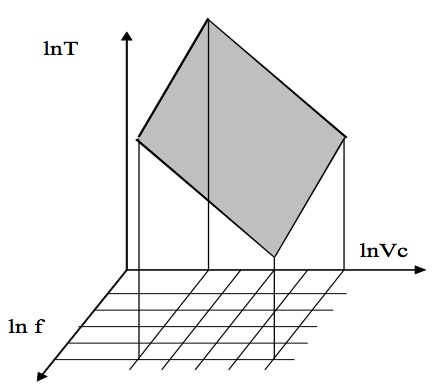
Fig.8 : Durée d’outil en fonction de Vc et f

Fig.8 : Durée d’outil en fonction de Vc et f

Si l'on désire aussi étudier l'influence de la pénétration en prenant 5 valeurs pour ce nouveau facteur, il faudrait alors réaliser 125 essais, ceux-ci correspondent à un plan factoriel complet.



3.1. Plans factoriels complets

Définition

L'étude d'un plan complet consiste à étudier toutes les combinaisons possibles des facteurs pris en considération dans l'expérience. Pour k facteurs à n niveaux, le plan complet comporte donc nk essais. 

Pour illustrer l'étude des plans complets nous allons prendre comme exemple l'influence des conditions cinématiques de l'usinage (Vc et f) sur la durée d'outil T avec seulement 2 niveaux par facteur. Le plan complet comporte donc 4 essais (fig.9).

La réponse, caractéristique de la durée d'outil, diminue de 1 quand l'avance passe du niveau 1 au niveau 2 ; elle diminue de 1,5 quand la vitesse passe du niveau 1 au niveau 2. 

L'effet global de l'avance est de -1 et celui de la vitesse est -1,5.

tab1

fig.9

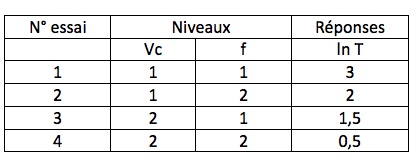
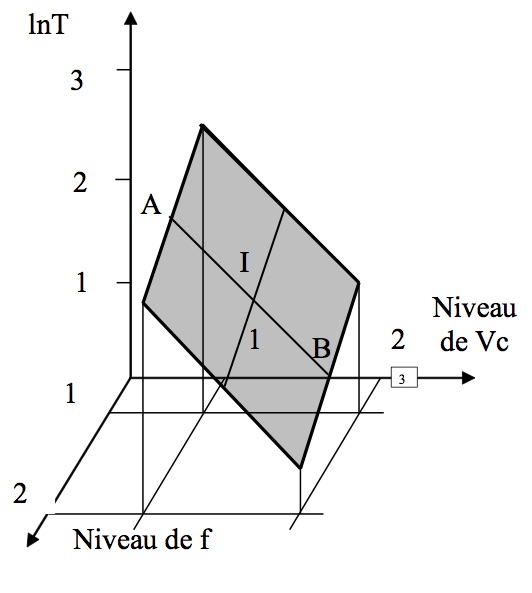
Fig.9


Calcul des effets moyens

Les effets moyens sont calculés par rapport à la moyenne générale des essais qui correspond au point central du domaine de validité des facteurs (point I sur Fig. 10)

L'effet moyen de l'avance au niveau 2 est obtenu par :

Ef2 = moyenne des réponses pour f au niveau 2 – moyenne générale ;

de même :

Ef1      = moyenne des réponses pour f  au niveau 1 – moyenne générale ;

EVc2    = moyenne des réponses pour Vc au niveau 2 – moyenne générale ;

EVc1    = moyenne des réponses pour Vc au niveau 1 – moyenne générale.

Exemple précédent : 

Moyenne = 1/4 * (3+2+1,5+0,5) = 1,75

EVc1 = 1/2 * (3+2)-1,75 = 0,75

EVc2 = 1/2 * (1,5+0,5)-1,75 = -0,75

Ef1 = 1/2 * (3+1,5)-1,75 = 0,5

Ef2 = 1/2 * (2+0,5)-1,75 = -0,5

Ef1 = -Ef2 et EVc1 = -EVc2. Il y a donc une seule valeur indépendante soit un seul degré de liberté par facteur.

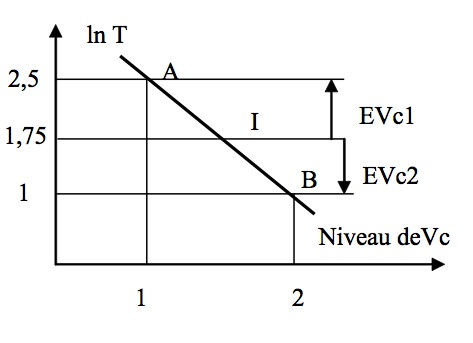
fig.10

Fig.10

Calcul de la durée d'outil théorique

Connaissant les effets moyens des facteurs Vc et f, il est alors facile de calculer la durée d'outil théorique, c'est-à-dire la durée que l'on devrait mesurer si celle-ci ne dépendait que des effets moyens des facteurs pris en compte.

Exemple : essai n°2 (Vc au niveau 1 et f au niveau 2)

Durée théorique = moyenne générale + EVc1 + Ef2 =1,75 + 0,75 – 0,5 = 2

Dans cet exemple simple, la durée théorique est identique à la durée mesurée car nous avions choisi volontairement des valeurs de durées mesurées telles que les points soient situés sur le plan T(Vc,f), (fig.10).

En réalité, compte tenu de la précision du modèle de la loi d’usure et des dispersions liées aux résultats des essais d'usure, il existe des écarts entre les valeurs mesurées et théoriques.

Graphe des effets moyens

Le graphe des effets moyens est une représentation graphique des résultats du plan d'expériences (fig.11). Le sens de variation indique si les facteurs agissent de façon positive ou négative sur la réponse (ln(T)), la pente permet d'identifier rapidement le facteur le plus influent.

Dans notre exemple, les 2 facteurs (Vc et f) ont des effets défavorables sur la durée de vie de l'outil et le facteur Vc est le plus influent.

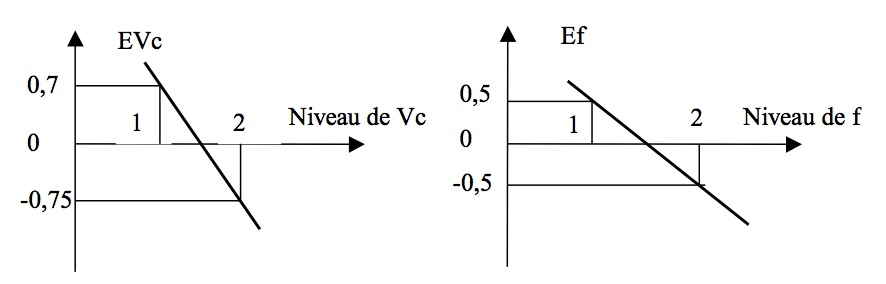
fig.11

Fig.11 Graphe des effets moyens 

Notion d'interaction.

Les interactions sont les phénomènes les plus difficiles à interpréter. La figure 12 illustre cette notion.

Le cas (a) correspond à l'exemple précédent, il n'y a pas d'interaction car l'effet sur la durée d'outil est de –1.5 lorsque le facteur Vc passe du niveau 1 au niveau 2, et ceci indépendamment du niveau du facteur f.

Le cas (b) montre un phénomène d'interaction, il y a une distorsion de la surface de réponse d'autant plus grande que l'interaction est importante.

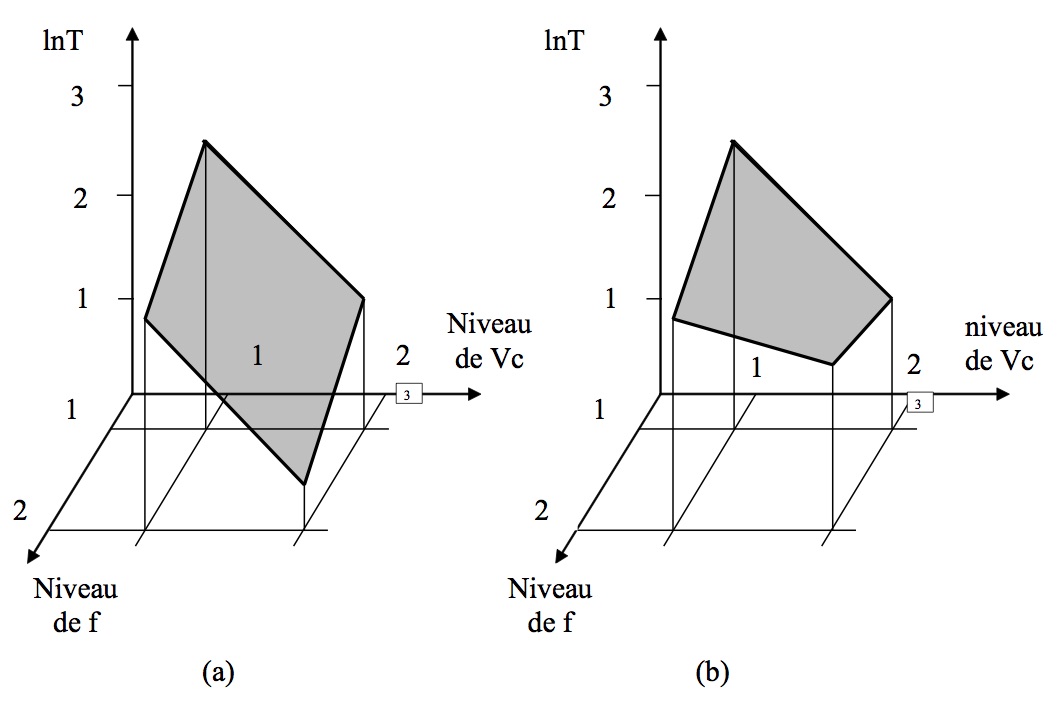
fig.12 notion d'interaction

Fig.12 Notion d'interaction


Plan d'expérience fractionnaires. 

Dans les plans factoriels chaque nœud du maillage donne lieu à un essai, le nombre d'essais peut très vite devenir incompatible avec les contraintes industrielles.

La méthode des plans d'expériences fractionnaires permet de réduire de façon significative le nombre d'essais ; le principe consiste à n'étudier que certains points du maillage.

Ces plans doivent vérifier deux conditions : 

  •   Première condition :

Ils doivent être orthogonaux pour calculer les effets d'un facteur indépendamment des autres facteurs. Il y a orthogonalité si à chaque niveau d'un facteur, tous les niveaux des autres facteurs sont associés le même nombre de fois dans le plan d'expériences.

Exemple : table de TAGUCHI L9(33), 9 essais, 3 facteurs (Vc, f, ap) avec 3 niveaux (1, 2, 3).

tab.2

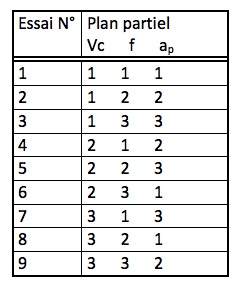
Tab.2

Essais 1, 2, 3 : Lorsque Vc est au niveau 1, f est une fois aux niveaux 1, 2 et 3 et de même pour le facteur a.

Essais 2, 5, 8 : Lorsque f est au niveau 2, Vc est une fois aux niveaux 1, 2, 3 et de même pour le facteur a.

Etc……

  • Deuxième condition :

Condition sur le nombre de degrés de liberté. C'est le nombre de valeurs qu'il est nécessaire de calculer pour connaître l'ensemble des coefficients du modèle ; il est donc nécessaire de faire autant d'essais qu'il y a de degrés de liberté dans le modèle.

Exemple précédent :

    •  soit le modèle T = Moyenne générale + EVc + Ef + Eap ,
    •  avec 3 niveaux pour chaque facteur.

Pour déterminer les effets moyens du facteur Vc pour les trois niveaux, il suffit de calculer les effets moyens pour 2 niveaux car :

EVc1 + EVc2 + EVc3 = 0

Il y a donc 2 degrés de liberté pour EVc, de même pour Ef et Eap. 

Le nombre total de degrés de liberté de ce modèle est donc de 1+2+2+2 = 7.


Détermination de la loi d'usure des outils de coupe.

La loi d'usure des outils de coupe définit la variation du temps effectif de coupe T(min) en fonction des facteurs principaux de l'usinage : la vitesse de coupe Vc (m/min), l'avance par tour f (mm/tr) et la pénétration ap (mm). Pour les valeurs usuelles de ces trois facteurs, la loi d'usure est généralement représentée par le modèle suivant:

\( T = K a_p^l f^m V_c^n \)

où K est un coefficient fonction du couple outil-pièce et du critère d'usure adopté, les exposants l, m, n dépendent essentiellement du matériau outil.

Par le changement de variables : A = ln(ap), F = ln(f),  V = ln(Vc), on obtient le modèle linéaire suivant :

\( ln(T) = ln(K)+l A + mF + n V \)

D'autre part, si dans le modèle :

ln(T) = moyenne générale +EA+EF+EV

les effets moyens EA, EF et EV varient linéairement respectivement en fonction des facteurs A, F et V, on peut écrire :

EA = a1 A + b1

EF = a2 F + b2

EV = a3 V + b3

et ln(T) = (Moyenne + b1 + b2 + b3) + a1 A + a2 F + a3 V.

En comparant les deux modèles de la loi d'usure, il vient :

ln(K ) = Moy + b1 + b2 + b3

l = a1

m = a2

n = a3

Le calcul des effets moyens EA, EF et EV des 3 facteurs A, F et V permet donc de déterminer aisément les valeurs des coefficients du modèle de la loi d'usure des outils de coupe.