Document ressource - Usure des outils de coupe

• Coûts annexes par pièce C_a, indépendants des conditions de coupe. Ce sont essentiellement les frais résultant des opérations annexes effectuées avant ou après l'usinage de chaque pièce (montage, démontage, réglages, contrôle,…), et qui sont indépendants des conditions de coupes adoptées. Pour un travail déterminé, ces dépenses par pièce sont constantes, et fonction du coût horaire (ou "minute") du poste de travail.
  
• Coûts d'usinage par pièce C_u : \( C_u = p_u . t_u \), avec p_u le coût machine par minute et t_u le temps d’usinage. Le coût minute du poste comprend :
• les coûts de main-d'œuvre d'usinage (personnel conduisant la machine) ;
• l’amortissement de la machine (ventilation des frais d'achat et installation par heure d'utilisation, déterminée a priori d'après la durée de vie probable de la machine) ;
• les frais de maintenance, et divers.
• Coût d'outillage C_o (quote-part nécessaire pour l'usinage d'une pièce) : \( C_o = \frac{p_o}{T/t_u} \), avec p_o le prix de revient d’une arête de coupe (€) et T la durée de vie de l’outil (min). Le prix de revient d’une arête de coupe comprend :
• les frais d'achat des outils, l'amortissement des porte-outils ;
• les frais d'affûtage, l'amortissement du matériel d’affûtage ;
• les frais de réglage.

• Coût du changement d'arête C_c : \( C_c = t_c . \frac{p_u}{T/t_u} \). Il dépend du temps de changement d’arête t_c et du coût minute du poste de travail.

Soit globalement

\( C_g = C_a + C_u + C_o + C_c = C_a + p_u . ( t_u + t_u \frac{t_c + Z}{T}) \)

avec Z = p_o/p_u, qui caractérise l'importance relative des coûts d'outillage et d'usinage, laquelle dépend des conditions particulières de chaque poste de travail.

Le temps d'usinage d'une pièce t_u et la durée effective de coupe T de l'outil sont liés aux conditions de coupe par les relations :

\( t_u = \frac{L}{N.f} \)

Le modèle de Taylor généralisé donne:

\( T = K . a_p^1 . f^m . V_c^n \)

d'où

\( C_g = C_a + \frac{p_u L x D}{1000 f V_c} (1+(t_c+Z)/C_V V_C^n) \)

avec \( C_v = K a_p^1 f^m \).

Pour une profondeur de passe donnée (a_p = a_p1), l'évolution du coût global de fabrication en fonction de l'avance et de la vitesse de coupe est représentée graphiquement par une surface en forme de gouttière dont le fond est continuellement décroissant quand l'avance croît : le minimum du coût est alors obtenu pour la valeur maximale possible de l'avance (Fig.4).

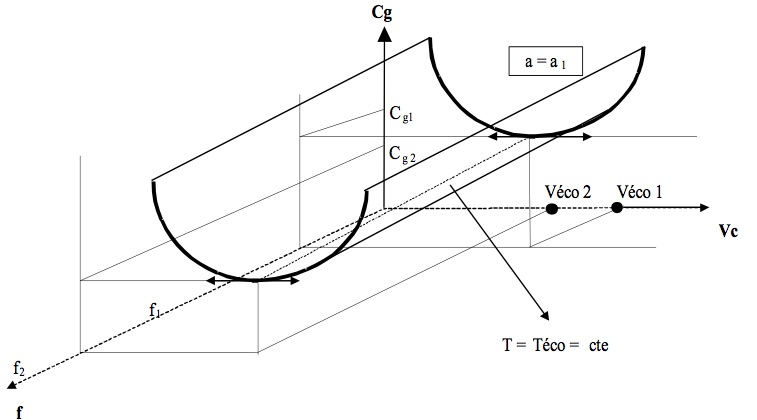
Fig.4: Coût global en fonction de la vitesse de coupe et de l’avance

Pour une avance donnée ( f = f₁), les évolutions du coût global et des différents coûts partiels sont indiqués sur la Fig.5.

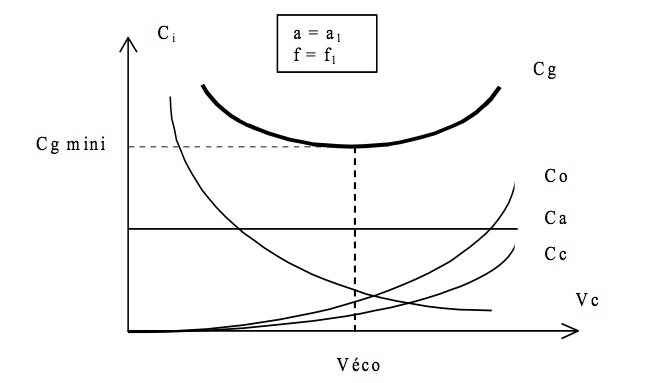
Fig.5 : Coûts en fonction de la vitesse de coupe

Le coût global par pièce est minimal pour la valeur de la vitesse de coupe V_ec dite "économique", solution de l'équation différentielle :

\( \frac{\partial C_g}{\partial V_c} = 0 \) pour a_p=a_p1 et f=f_1, soit 

\( V_{ec} = \left \lbrack \frac{(-n-1). (t_c+p_o/p_u)}{C_v} \right \rbrack ^{1/n} \)

avec \( C_v = K a_{p1}^l f_1^m \).

La durée effective de coupe de l'outil correspondante, dite "économique" est :

\( T_{ec} = (-n-1) . (p_o/p_u + t_c) \)

La valeur de la durée de coupe économique T_ec est indépendante de la constante C_v, elle n'est donc pas fonction du matériau usiné, ni de la géométrie du copeau.

Par contre, T_ec dépend de l'exposant n, c'est-à-dire du matériau outil (fig. 6). Les valeurs de T_ec pour chaque matériau outil sont en moyenne :

• Acier rapide : T_ec ∈ [40 ; 120]min
• Carbure : T_ec ∈ [15 ; 40]min
• Céramique : T_ec ∈ [5 ; 15]min

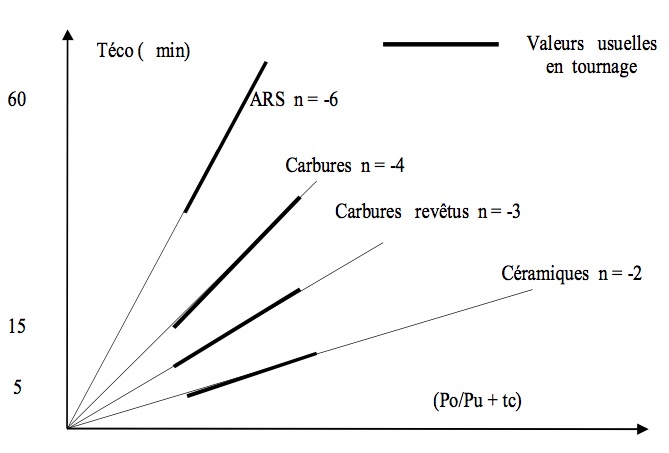
Fig.6 : \( T_{ec} = f(\frac{p_o}{p_u} + t_c) \)

Ainsi, les valeurs des vitesses de coupe indiquées dans les tableaux des données correspondent généralement à une durée effective de coupe voisine de l'optimum économique. La détermination des vitesses de coupe pour une durée effective de coupe différente se fait facilement à partir du modèle de Taylor.